婎杮偲丄擲傞偙偲
丂曌嫮偱傕壗偱傕丄婎杮偑戝帠偱偡丅搚戜偑偱偒偰偄側偄偺偵擄偟偄偙偲傪傗傠偆偲偟偰傕偆傑偔偄偒傑偣傫丅惉岟偟偰偄傞恖偼昁偢偲偄偭偰偄偄傎偳丄婎杮傪偒偪傫偲儅僗僞乕偟偰偄傑偡丅
丂偨偲偊偽悢妛偺婎杮偼丄侾偮偼寁嶼椡傗恾傪偐偔椡丄傕偆侾偮偼岞幃側偳廳梫帠崁偺乽堄枴偲偱偒曽偲巊偄曽乿傪棟夝偡傞偙偲偱偡丅
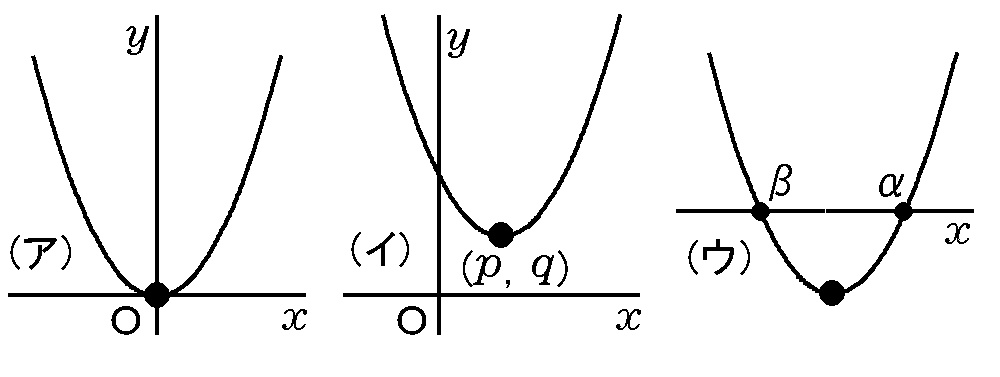 丂俀師娭悢偺婎杮偼丄拞俁偱廗偆嘆y亖ax俀偺僌儔僼偱偡乮壓恾偺傾乯丅偙傟偼捀揰偑尨揰丄幉偑y幉(x亖侽)偺僌儔僼偱偡丅偙傟傪暯峴堏摦偟偰捀揰偑(p丆q)偵側傞傛偆偵偡傞偲丄嘇y亖a(x亅p)俀亄q偲偄偆僌儔僼偵側傝傑偡乮恾偺僀乯丅偙偺暯峴堏摦偺峫偊曽偑彮偟擄偟偄偺偱偡偑丄傢偐傞偲偙傟埲奜偺宍偺僌儔僼傕慡晹暯峴堏摦偱偒傞傛偆偵側傞偺偱丄戝帠側偲偙傠偱偡乮悢嘦丒悢嘨偱偙偺棟孅偼偲偰傕栶偵棫偪傑偡乯丅
丂俀師娭悢偺婎杮偼丄拞俁偱廗偆嘆y亖ax俀偺僌儔僼偱偡乮壓恾偺傾乯丅偙傟偼捀揰偑尨揰丄幉偑y幉(x亖侽)偺僌儔僼偱偡丅偙傟傪暯峴堏摦偟偰捀揰偑(p丆q)偵側傞傛偆偵偡傞偲丄嘇y亖a(x亅p)俀亄q偲偄偆僌儔僼偵側傝傑偡乮恾偺僀乯丅偙偺暯峴堏摦偺峫偊曽偑彮偟擄偟偄偺偱偡偑丄傢偐傞偲偙傟埲奜偺宍偺僌儔僼傕慡晹暯峴堏摦偱偒傞傛偆偵側傞偺偱丄戝帠側偲偙傠偱偡乮悢嘦丒悢嘨偱偙偺棟孅偼偲偰傕栶偵棫偪傑偡乯丅丂偦偆傗偭偰偱偒偨嘇偺幃傪揥奐偡傞偲丄嘊y亖ax俀亄bx亄c 偲偄偆宍偵側傝傑偡丅偙偺宍偼y傗x偺抣傪戙擖偟偰寁嶼偡傞偺偵偼曋棙側偙偲偑懡偄偱偡乮偦偆偱側偄応崌傕偁傝傑偡乯丅偙偙偐傜偝傜偵場悢暘夝偱偒傞応崌偵偼嘋y亖a(x亅兛)(x亅兝) 偲偄偆宍偵偡傞偙偲傕偱偒傑偡丅偙偺幃偼y亖a(x亅兛)(x亅兝)亖侽偲偟偰傒傞偲乽y亖侽偵側傞偲偒偺x偺抣偑兛丆兝乿偲偄偆堄枴偵側傝傑偡丅偙傟傪恾偵昞偡偲恾偺僂偲側傝丄兛偲兝偼僌儔僼偲x幉偲偺岎揰傪昞偡偙偲偑傢偐傝傑偡丅嘊偺幃傪嘋偺宍偵偱偒側偄乮幚悢偵側傞兛丄兝偑側偄乯偲偒偼丄偙偺僌儔僼偑x幉偲岎傢傜側偄偙偲偵側傝傑偡偑丄偙偺偲偒a(x亅兛)(x亅兝)亖侽偼幚悢夝傪帩偨側偄偺偱曽掱幃偺敾暿幃亙侽偲側傝傑偡丅偮傑傝敾暿幃傪媮傔傞偙偲偱丄僌儔僼偲x幉偺岎揰偑偁傞偺偐偳偆偐傪挷傋傞偙偲偑偱偒傞偺偱偡丅
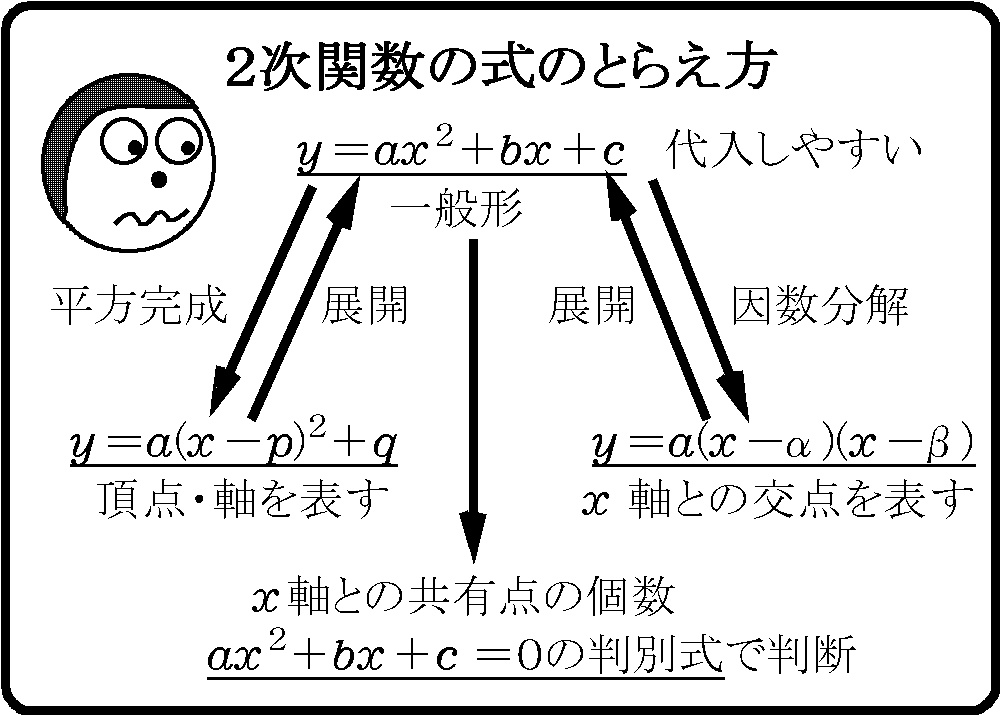 丂僑僠儍僑僠儍彂偒傑偟偨偑丄偙偙傑偱偑俀師娭悢偺乽婎杮乿偱偡丅幃偺堄枴偺棟夝丄幃傪曄宍偡傞寁嶼椡丄偒傟偄偵僌儔僼傪偐偔椡乧乧偙傟傜偑偱偒傞偙偲偑廳梫偱偡丅傛偔塃偺傛偆側僷僞乕儞傪娵埫婰偟傛偆偲偡傞恖偑偄傑偡偑丄側偤偦偆側傞偐偑傢偐傜偢偵宍偩偗妎偊傞偲丄妛峑偺僥僗僩偵偼偁傞掱搙懳墳偱偒偰傕擖帋栤戣偱偼敿暘偔傜偄偟偐捠梡偟傑偣傫丅僙儞僞乕帋尡側偳偼妱崌僷僞乕儞偑寛傑偭偰偄偰懳嶔偑棫偰傗偡偄偺偱偡偑丄偦傟偱傕偙偙偵彂偄偨偙偲偑傎傏慡晹弌偰偔傞偟丄栤戣偺忦審偑傗傗偙偟偄偺偱丄堄枴傪棟夝偟偨忋偱巊偄暘偗傞昁梫偑偁傝傑偡丅
丂僑僠儍僑僠儍彂偒傑偟偨偑丄偙偙傑偱偑俀師娭悢偺乽婎杮乿偱偡丅幃偺堄枴偺棟夝丄幃傪曄宍偡傞寁嶼椡丄偒傟偄偵僌儔僼傪偐偔椡乧乧偙傟傜偑偱偒傞偙偲偑廳梫偱偡丅傛偔塃偺傛偆側僷僞乕儞傪娵埫婰偟傛偆偲偡傞恖偑偄傑偡偑丄側偤偦偆側傞偐偑傢偐傜偢偵宍偩偗妎偊傞偲丄妛峑偺僥僗僩偵偼偁傞掱搙懳墳偱偒偰傕擖帋栤戣偱偼敿暘偔傜偄偟偐捠梡偟傑偣傫丅僙儞僞乕帋尡側偳偼妱崌僷僞乕儞偑寛傑偭偰偄偰懳嶔偑棫偰傗偡偄偺偱偡偑丄偦傟偱傕偙偙偵彂偄偨偙偲偑傎傏慡晹弌偰偔傞偟丄栤戣偺忦審偑傗傗偙偟偄偺偱丄堄枴傪棟夝偟偨忋偱巊偄暘偗傞昁梫偑偁傝傑偡丅丂偙偆傗偭偰尒偰偄偔偲杮摉偵戝曄偦偆偱偡偑丄幚嵺偵偼暥宯偺恖偑庴偗傞悢妛偺擖帋栤戣偼乮僙儞僞乕帋尡傕娷傔偰乯偙偺婎杮偩偗偱俆乣俇妱偔傜偄偲傟傞偺偱偡丅傗偝偟偄偲偙傠側傜偙傟偩偗偱崌奿偟傑偡丅偦偆偱側偔偰傕俈妱偲傟偽偩偄偨偄崌奿揰側偺偱丄夝偐側偗傟偽偄偗側偄墳梡栤戣偼慡懱偺侾妱掱搙偵側傝傑偡丅偙傟偼懠偺壢栚偱傕傎傏摨偠偩偲巚偭偰偐傑偄傑偣傫丅
丂墳梡栤戣偲偄偭偰傕丄嬨戝偲偐搶戝偲偐偺擄娭峑偱側偗傟偽丄傎偲傫偳偑婎杮偺慻傒崌傢偣偵偡偓傑偣傫丅嶰妏娭悢偲俀師娭悢傪慻傒崌傢偣偨傝丄場悢暘夝偲柦戣乮昁梫忦審偲偐乯傪慻傒崌傢偣偨傝偟偰丄壗傪偳偆巊偭偨傜偄偄偺偐傢偐傝偵偔偔偟偰崿棎偝偣傛偆偲偄偆傢偗偱偡丅
丂偩偐傜偁偲偼偦偆偄偆擖帋栤戣傪側偑傔偰乽偙傟偼婎杮偺壗偲壗傪慻傒崌傢偣偰巊偭偨傜偄偄偺偐乿傪峫偊傞偙偲偱偡丅偙傟偼崅峑擖帋偱偼偁傑傝偟側偐偭偨楙廗偱丄偩偐傜拞妛偺帪傛傝帪娫偑偐偐傝傑偡丅嵟弶偼壗偑壗偩偐傢偐傜側偄偐傕偟傟傑偣傫丅夝愢傪撉傫偩傝愢柧傪暦偄偨傝偟偰傕偄偄偺偱偡偑丄帺暘偱栤戣傪側偑傔側偑傜偠偭偔傝峫偊偰傒傞偙偲傕昁梫偱偡丅擄偟偄栤戣偵帪娫傪偐偗傞偺偼嬯偟偄偐傕偟傟傑偣傫偑丄傢偐偭偨偲偒偺偆傟偟偝傕奿暿偱偡丅僎乕儉偱嫮偄僉儍儔傪搢偡偺偑妝偟偄傛偆偵丄擄栤傪擲偭偰峫偊偰夝偗偨偲偒偵偼丄乽偱偒偨両乿偲嫨傃偨偄傎偳偺婌傃偑偁傝傑偡丅摿偵悢妛偵偼偦偆偄偆栤戣偑懡偄偲巚偄傑偡丅悢妛偑柺敀偄側傫偰巚偊側偄偲偄偆恖傕偄傞偱偟傚偆偑丄杮婥偱擄偟偄栤戣偵庢傝慻傫偱摎傑偱偨偳傝拝偗傟偽丄扤偩偭偰棟孅偱峫偊傞偙偲偺妝偟偝傪枴傢偊傞偺偱偡丅偣偭偐偔曌嫮偟偰偄傞偺偩偐傜丄偦偆偄偆宱尡傪崅峑偺偆偪偵宱尡偟偰傎偟偄偱偡丅僆僩僫偵側偭偰傕偦偆偄偆乽婎杮偲擲傝乿偑栶偵棫偮傫偱偡傛丅(2009/10/28)